Teori Linier - Rumus Soal
Keberadaan internet membuat siapa saja bisa mengakses berbagai informasi, maka tidak heran belakangan ini banyak sekali betebaran situs-situs yang membahas mengenai Teori Linier. Hal ini sangat logis mengingat di era pandemi ini, masyarakat kita lebih sering melakukan proses belajar mengajar secara daring. Baiklah sudah cukup basa-basinya, yuk langsung masuk ke pembahasan saja.
Penjelasan Lengkap Teori Linier
Hallo gaes pada artikel sebelumnya rumussoal.com sudah memberikan wawasan atau berbagi ilmu pengetahuan dari berbagai materi.
Namun kali ini rumussoal.com akan menyampaikan materi tentang Teori Linier pada perubahan sosial – lengkap dengan pengertian, fungsi, perkembangan, perubhan, dan contohnya supaya mudah dipahami.
Baiklah gaes untuk mempersingkat waktu langsung saja simak pembahasan dibawah ini yaaa…?
Pengertian Teori Linier

Teori linier ialah salah satu teori yang mempaparkan atau menjelaskan tentang perubahan sosial dan akan berkembang dan terus berekembang untuk menuju ke suatu arah atau titik tujuan tertentu.
Pengertian Fungsi Linier yang ke-2 adalah fungsi polinom yang variabelnya bebas dan mempunyai pangkat paling tinggi di antara satuan lainnya adalah satu
Fungsi Teori Linier
Fungsi linier adalah fungsi yang sangat penting dan paling sederhana sebab hanya memiliki satu variabel bebas.
Dan berpangkat satu pada bagian variabel bebas itu,sehingga sering disebut dengan fungsi berderajat satu (1)
Bentuk umum persamaan pada linier ialah:
b =gradien atau kemiringan a = intersep
Y = a + bX
Intersep a adalah awal tiitk potong di antara fungsi linier dengan sumbu Y.
Gradien b yaitu adalah kemiringan dari fungsi linier terhadap dari sumbu X.
- Jika b bernilai nol adalah digambarkan garis yang sejajar juga dengan sumbu datar X.
- Jika b bernilai negatif adalah fungsi linier yang akan digambarkan garis dari kiri atas menuju ke kanan bawah.
- Jika b bernilai positif adalah fungsi linier akan digambarkan garis dari kiri bawah ke kanan atas.
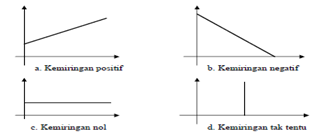
A. Penggambaran fungsi linier
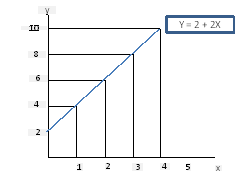
Jika b bernilai positif : Y = 2 + 2X maka kurva yang bergerak dari kiri bawah ke kanan atas
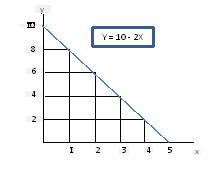
Jika b bernilai negatif : Y = 10 – 2X maka kurva yang bergerak dari kiri atas ke kanan bawah
Didalamnya akan mengambarkan tentang hubungan input atau output transduser sinyal contohnya seperti Radio yang nantinya akan merubah input sinaptik dan akan menjadi respos.
Sebab sudah bnayak sekali aplikasi didalam teori informasi, fisika dan juga teknik terdapat juga ama altetnatif.
Untuk fungsi respon linier ini sendiri sangat spesifik contohnya seperti kerentanan, respon pada impuls dan juga impedansi.
Dan mari kita lihat juga apa itu fungsi transfer.
Pada konsep fungsi Green atau yang di sebut juga dengan solusi fundamental dari 2 gabungan persamaan diferensi biasa terikat atau berkaitan sangat kuat.
Baca Juga: Soal UAS Matematika SD Kelas 2
Teori Perkembangan Linier
Teori ini merupakan teori yang percaya bahwa perubahan sosial dapat di arahkan ke titik tujuan tertentu.
Misalnya seperti perubahan sosial dari masyarakat tradisional menjadi masyarakat yang modern.
Contohnya:
Perkembangan bangsa indonesia dari jaman penjajahan mempertahankan kemerdekaan sampai saat ini.

Jika kita ibaratkan maka reori linier ini yang beranggapan bahwa pada perubahan sosial yang akan terjadi memberikan kemajuan tersendiri bagi semua masyarakat (grafis naik).
Teori perubahan melingkar (siklus)
Teori ini sangatlah beranggapan jika pada perubahan sosial pada semua masyarakat merupakan sesuatu yang tidak bisa direncanakan ataupun di arahkan kembali.
Misalnya perubahan pada mode pakaian atau gaya hidup kita sehari-hari.

Baca Juga: Hikayat Bakhtiar
Program Linear
Program linear adalah suatu metode penentuan nilai optimum dari suatu persoalan linear.
Nilai optimum dapat di peroleh dari nilai dalam suatu himpunan penyelesaian persoalan linear.
Terdapat fungsi linear yang sering di sebut sebagai pungsi objektif.
Persyaratan, batasan, dan kendala dalam persoalan linear merupakan sistem pertidaksamaan linear.

Modal matematika program linear
Model matematika merupakan pernyataanyang menggunakan penggubah dan notasi matematika.
Sebagai ilustrasi,produsen sepatu, membuat 2 model sepatu menggunakan 2 bahan yang berbeda.
komposisi model pertama terdiri dari 200 gram bahan pertama dan 150gram bahan kedua.
Sedangkan komposisi model kedua terdiri dari 180 gram bahan pertama dan 170gram bahan kedua.
persedian di gudang bahan pertama 72 kg dan bahan kedua 64 kg, harga model pertama adalah Rp.500.000.00.
Model pada bahan kedua Rp.400.000.00, jika disimpulkan atau di sederhanakan dalam bentuk tabel sebagai berikut:

Dengan pengubah dari jumlah optimal model 1 ialahx dan model 2 adalah y, dan dapat dihasil penjualan optimal adalah f(x, y) = 500.000x + 400.000y. Dengan syarat:
- Jumlah maksimal bahan pertama ialah 72.000 gr, maka 200x + 180y ≤ 72.000.
- Jumlah maksimal bahan kedua ialah 64.000 gr, maka 150x + 170y ≤ 64.000
- Masing-masing model dapat terbuat.
Model matematika untuk mendapat jumlah penjualanyang maksimum adalah:
Maksimum f(x, y) = 500.000x + 400.000y
Syarat:
- 200x + 180y ≤ 72.000
- 150x + 170y ≤ 64.000
- x ≥ 0
- y ≥ 0
Baca Juga: Aturan Angka Penting
Nilai Dari optimum fungsi objektif
Fungsi objektif yakni fungsi linear dan juga batasan batasan pertidaksamaan atau perbedaan linear yang mempunyai himpunan dalam penyelesaian.
Himpunan untuk penyelesaian yang ada yakni pada titik-titik dalam diagram cartesius yang kalau koordinatnnya disubsitusikan atau dimasukan ke dalam pungsi linear dapat memenuhi syarat yang berlaku.
Nilai dari optimum fungsi dalam objektif dari salah satu persoalan juga bisa di jumpai dengan cara menggunakan metode grafik.
Dengan cara kita melihat grafik dari fungsi objektifnya dan juga pada sebuah batasan-batasan yang dapat di tentukan pada letak dan juga titik-titik yang menjadi nilai optimumnya.
Langkah-langkahnya sebagai berikut:
- Menggambar dalam himpunan penyelesaian dari semua syarat-syarat yang sudah ada di cartesius.
- Memilih bagian titik-titik ekstrim yang perpotongan garis batasan dengan potongan garis batasan yang lainnya.
- Titik-titik ekstrim itu adalah himpunan penyelesaian dari batasannya yang memiliki kemungkinan yang besar membuat fungsi sebagai fungsi optimum.
Menggunakan garis selidik
Garis selidik didapat melalui fungsi objektif f(x, y) = ax + by dimana garis selidiknya merupakan: ax + by = Z
Membandingkan nilai pungsi tiap titik exstrim
Menyelidiki nilai optimum dari pungsi objektif juga dapat dilakukan dengan terlebih dahulu menentukan titik-titik potong dari garis-garis batas yang ada.
Pada titik-titik potong itu semua merupakan nilai exstrim yang berpotensi sangat besar mempunyai nilai maksimum pada salah satu titiknya.
Berdasarkan dari titik titik itu semua dapat ditentukan nilai maising-masing pada pungsinnya, kemudian di bandingkan lagi.
Nilai yang paling besar adalah nilai maksimum dan juga nilai terkecil merupakan nilai minimum.
Baca Juga: Kecepatan Sudut
Contoh Soal Program Linear dan Pembahasan
Contoh Soal 1
Tentukanlah nilai minimum dari f(x, y) = 9x + y pada daerah yang sudah dibatasi oleh 2 ≤ x ≤ 6, dan juga 0 ≤ y ≤ 8 serta x + y ≤ 7.
Pembahasan pertama:
- Langkah pertama menggambar grafiknya

- Langkah kedua menentukan titik ekstrim
Dari gambar diatas, ada 4 titik ekstrim, yaitu: A, B, C, D dan terdapat himpunan penyelesaiannya ada di area yang diarsir.
- Lankah tiga menyelidiki nilai optimum
Dari grafikdi atas diketahui titik A dan B mempunyai y = 0, sehingga kemungkinan dapat berubah menjadi nilai minimum.
ke-2 titik disubstitusikan kedalam f(x, y) = 9x + y agar dibandingkan.

Dengan membandingkan hal tersebut dapat disimpulkan bahwa titik A mempunyai nilai minimum 18.
Sekian sobat pembahasan dari rumussoal.com materi tentang, Teori Linier lengkap dengan perkembangannya, semoga materi yang sangat singkat ini mudah dipahami, dan juga bisa bermanfaat untuk kalian, sekian dan terima kasih.
Artikel Lainnya>>>>>
- Gejala Listrik Statis
- Satuan Rumus Debit
- Kecepatan Sudut
- Soal UAS Matematika SD Kelas 3
- Soal UAS Matematika SD Kelas 1
The post Teori Linier appeared first on RumusSoal.com.
ARTIKEL PILIHAN PEMBACA :
Comments
Post a Comment