Garis dan Sudut - Yuk Sinau

Garis dan Sudut - Sejauh ini mungkin ada diantara kita yang belum tahu tentang "Garis dan Sudut?" Namun tak perlu berkecil hati, karena di era sekarang sangat mudah untuk mencari informasi apa saja, buktinya Anda menemukan situs Chip Online ini. Tentu Anda tidak secara kebetulan tiba-tiba berada di situs ini bukan? Kami yakin demikian adanya.

Bisa jadi beberapa waktu lalu Anda mengetik kata 'Garis dan Sudut' di google dan menemukan situs ini berada di urutan atas pencarian Anda. Untuk itu kami ucapakan selamat datang di situs chipcoid. blogspot. com yang merupakan situs yang berisi berbagai informasi terkait pendidikan, pengetahuan, materi pelajaran, tips n trik, tutorial dan banyak lagi lainnya. Nah kami sudah merangkum informasi terkait Garis dan Sudut, yuk langsung disimak saja.

Pembahasan Lengkap Garis dan Sudut

Garis dan Sudut merupakan salah satu materi dalam matematika yang akan kita pelajari di bangku kelas 7 SMP. Nah, kali ini kita akan mempelajari berbagai hal yang berkaitan dengan garis dan sudut.

Mulai dari hubungan antara dua buah garis, jenis-jenis sudut, sifat-sifat sudut, dan juga satuan yang digunakan untuk sudut.

Selengkapnya simak baik-baik ulasan berikut ini.

Garis

Garis adalah suatu susunan titik-titik (bisa tak hingga) yang saling bersebelahan serta berderet memanjang ke dua arah (kanan/ kiri, atas/ bawah).

Kedudukan dua buah Garis

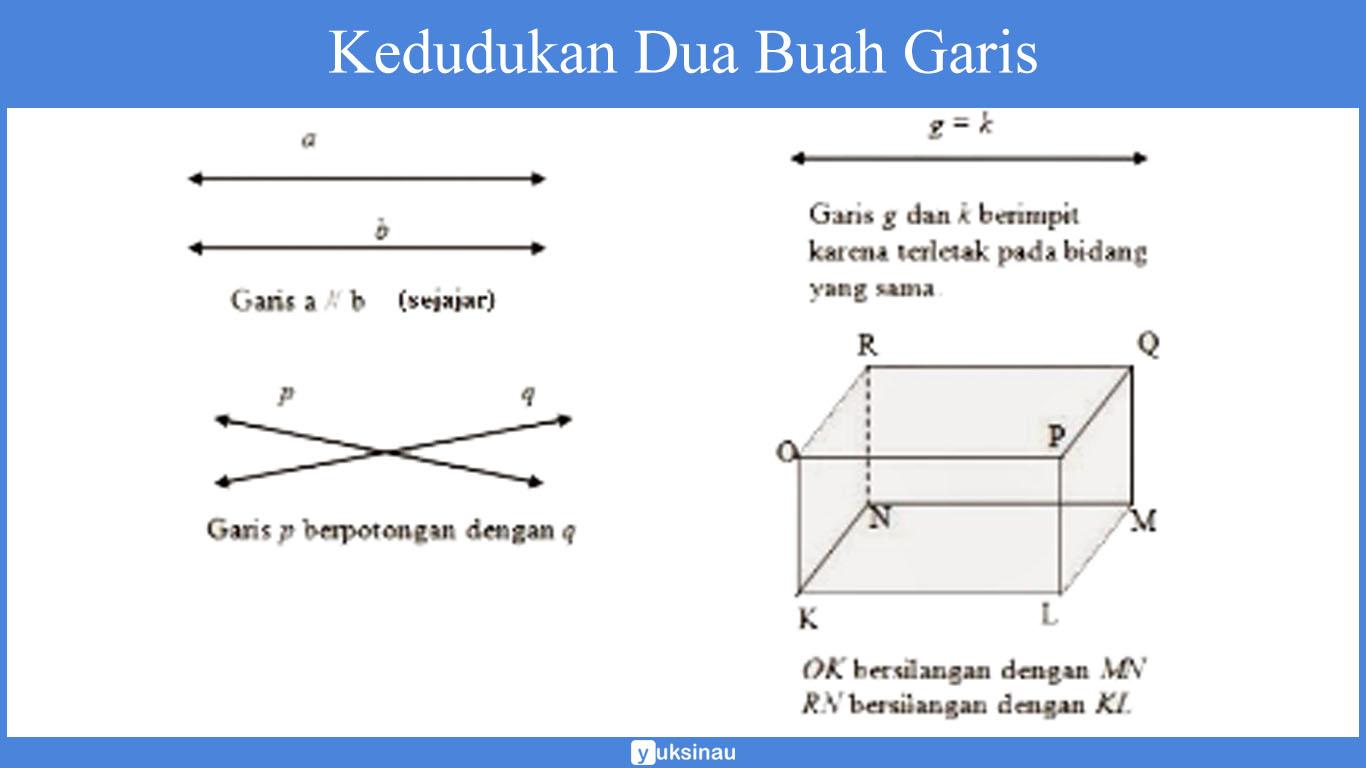
Garis Sejajar

Dua Garis Sejajar yaitu jika garis tersebut berada dalam satu bidang datar serta tidak akan pernah bertemu atau berpotongan apabila garis tersebut diperpanjang hingga tak berhingga.

Lambang dari garis sejajar yaitu (//)

Dua garis disebut saling sejajar apabila dua garis tersebut tberada pada satu bidang atau perpanjangannya tidak akan pernah berpotongan.

Adapun beberapa sifat dari garis sejajar, antara lain:

• Melewati suatu titik diluar garis, bisa dibuat tepat satu garis lain yang sejajar dengan garis tersebut.
• Apabila terdapat su atugaris yang memotong salah satu dari dua garis yang sejajar, maka garis tersebut akan memotong garis kedua.
• Apabila suatu garis sejajar dengan garis lainnya, maka kedua garis tersebut juga akan saling sejajar satu sama lain

Garis Berpotongan

Dua buah garis akan disebut berpotongan jika kedua garis tersebut mempunyai sutau titik potong atau biasa disebut dengan titik persekutuan.

Garis berhimpit

Dua buah garis akan disebut berhimpit jika kedua garis tersebut mempunyai setidaknya dua titik potong.

Sebagai contohnya: jarum jam pada saat menunjukkan pukul 12 pas. Maka kedua jarum jam tersebut akan saling berhimpit.

Garis Bersilangan

Dua buah garis bisa disebut saling bersilangan jika kedua garis tersebut tidak sejajar serta tidak berada pada satu bidang.

Untuk memahami beragam kedudukan garis di atas perhatikan pada gambar di bawah ini:

Sudut

Sudut merupakan hal yang dibentuk oleh pertemuan antara dua buah sinar ataupun dua garis lurus.

Sudut ini merupakan suatu daerah yang terbentuk dari sebuah sinar yang diputar pada pangkal sinar. Sudut dinotasikan dengan menggunakan simbol “∠”.

Pengertian Sudut

Di dalam ilmu matematika, sudut dapat diartikan sebagai sebuah daerah yang terbentuk karena adanya dua buah garis sinar yang titik pangkalnya saling bersekutu atau berhimpit.

Sudut dalam geometri merupakan suatu besaran rotasi suatu ruas garis dari satu titik pangkalnya ke posisi yang lain.

Selain itu, dalam bangun dua dimensi yang beraturan, sudut bisa juga didefiniskan sebagai ruang antara dua buah ruas garis lurus yang saling berpotongan. -sc: wikipedia

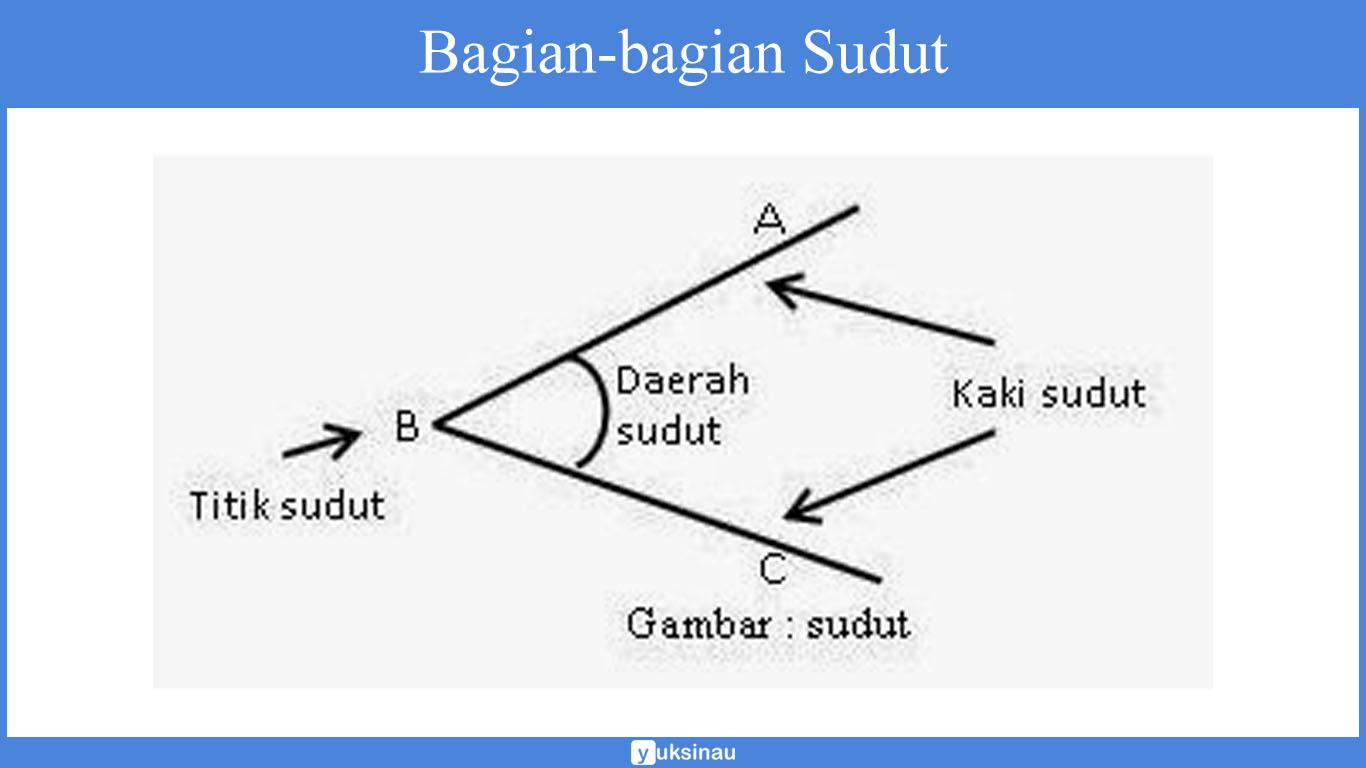
Bagian-bagian pada suatu sudut

Sudut mempunyai tiga bagian penting, diantaranya yaitu:

Kaki Sudut

Merupakan garis sinar yang membentuk sudut tersebut.

Titik Sudut

Merupakan titik pangkal atau  titik potong tempat berhimpitnya garis sinar.

Daerah Sudut

Daerah atau ruang yang terdapat diantara dua kaki sudut.

Untuk lebih jelasnya lihat gambar berikut:

Jenis-jenis Sudut

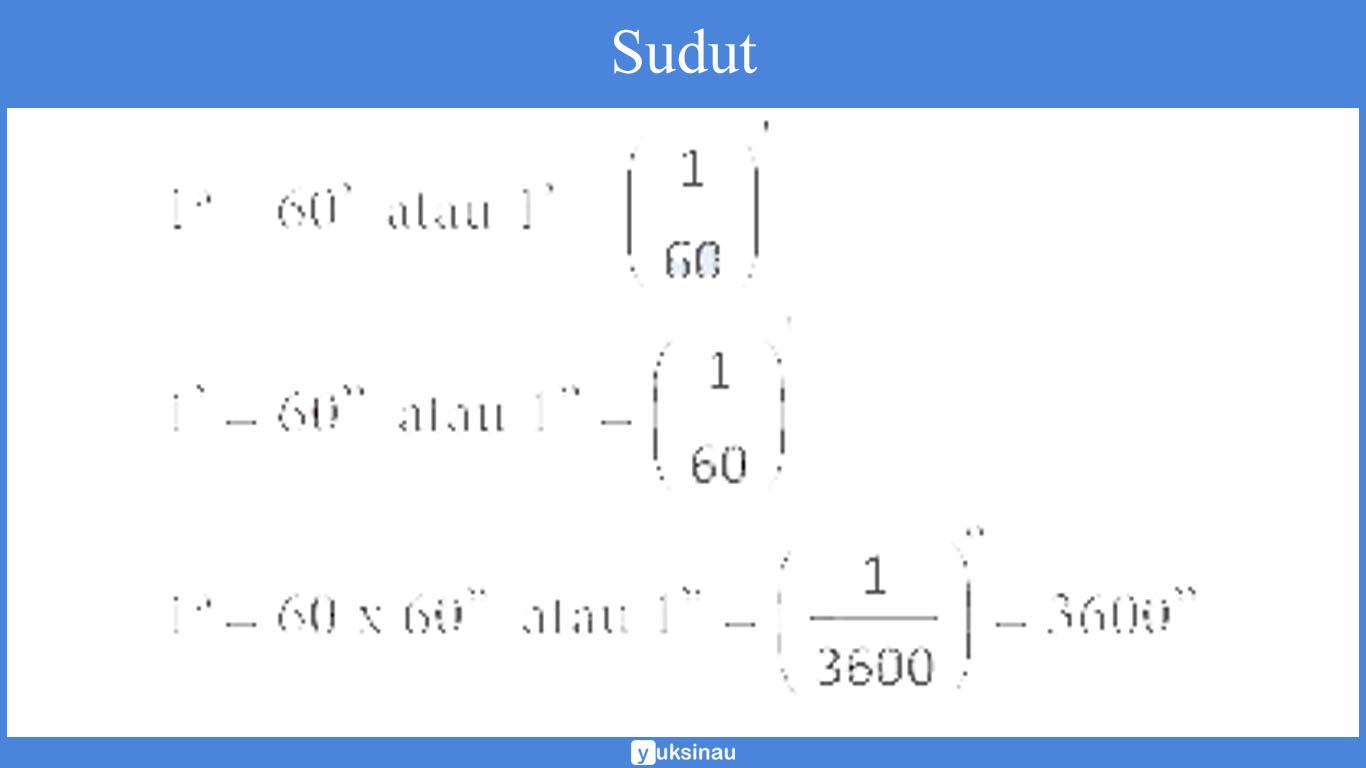
Untuk menyatakan besaran pada suatu sudut maka memakai satuan derajat (°), menit (‘), dan juga detik (“), di mana:

• Sudut yang besarnya 90° disebut sebagai sudut siku-siku.
• Sudut yang besarnya 180° disebut sebagai sudut lurus.
• Sudut yang besarnya antara 0° serta 90° disebut sebagai sudut lancip.
• Sudut yang besarnya antara 90° serta 180° (90°< D < 180°) disebut sebagai sudut tumpul.
• Sudut yang besarnya lebih dari 180° serta kurang dari 360° (180° < D < 360°) disebut sebagai sudut refleks.
• Jumlah dua sudut yang saling berpelurus (bersuplemen) yaitu 180°. Sudut yang satu adalah pelurus dari sudut yang lain.
• Jumlah dua sudut yang saling berpenyiku (berkomplemen) yaitu 90°. Sudut yang satu adalah penyiku dari sudut yang lain.
• Apabila dua garis berpotongan maka dua sudut yang letaknya saling membelakangi titik potongnya disebut sebagai dua sudut yang saling bertolak belakang. Dua sudut yang saling bertolak belakang merupakan sudut yang sama besar.

Kedudukan Dua garis

Berikut adalah kedudukan dari dua garis, antara lain:

• Dua garis atau lebih disebut saling sejajar jika garis-garis tersebut berada pada satu bidang datar serta tidak akan pernah bertemu atau berpotongan apabila garis tersebut diperpanjang hingga tak berhingga.
• Dua garis disebut akan saling berpotongan jika garis tersebut terletak pada satu bidang datar serta memiliki satu titik potong.
• Dua garis disebut saling berimpit jika garis tersebut berada pada satu garis lurus, sehingga hanya terlihat satu garis lurus saja.
• Dua garis disebut saling bersilangan jika garis-garis tersebut tidak berada pada satu bidang datar serta tidak akan berpotongan jika diperpanjang.

Hubungan antar Sudut

Sudut Berpenyiku

Jika terdapat dua buah sudut yang saling berhimpitan serta membentuk sudut siku-siku, maka sudut yang satu akan menjadi sudut penyiku untuk sudut yang lain sehingga kedua sudut tersebut disebut sebagai sudut yang saling berpenyiku (komplemen).

Berikut adalah gambar untuk sudut berpenyiku:

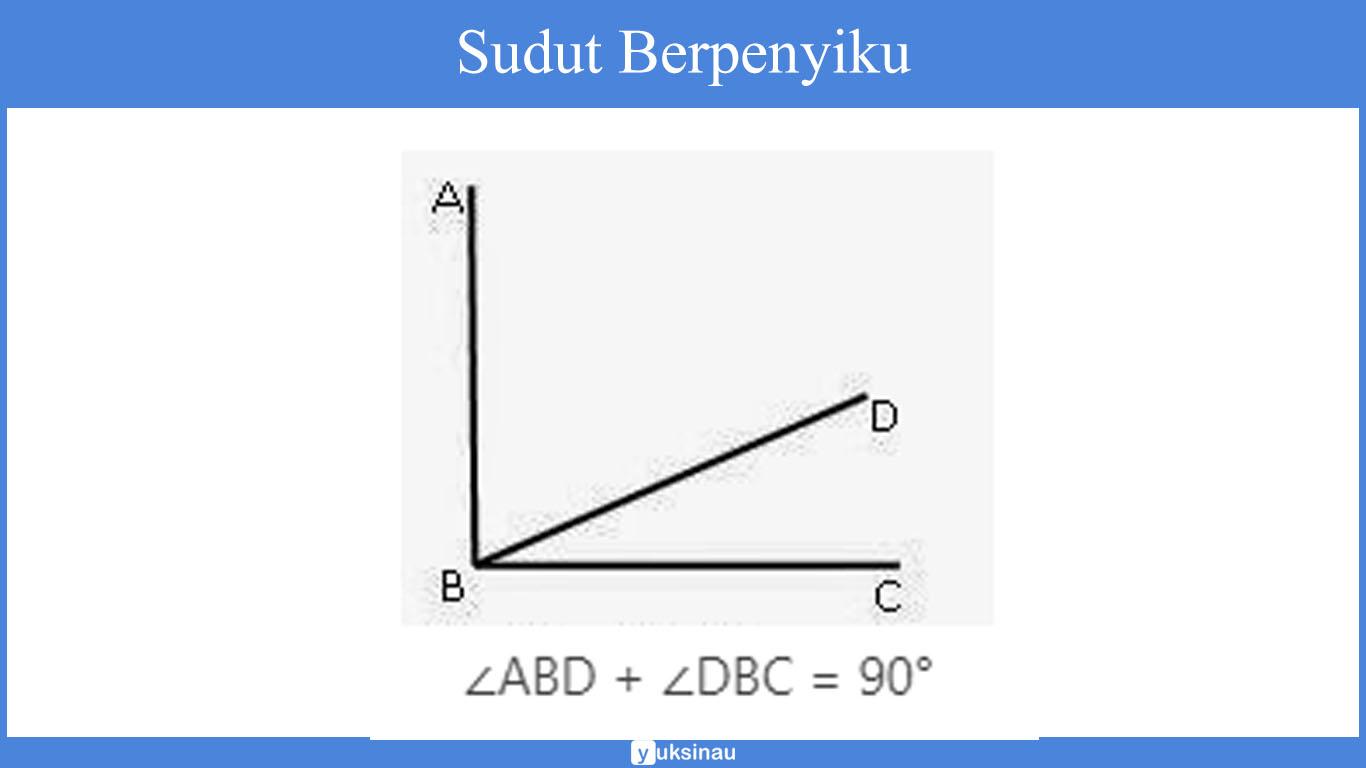
Jumlah dua sudut yang saling berpenyiku (berkomplemen) yaitu 90°. Sudut yang satu adalah penyiku dari sudut yang lain.

Sudut Berpelurus

Jika terdapat dua buah sudut yang saling berhimpitan serta saling membentuk sudut lurus maka sudut yang satu akan menjadi sudut pelurus untuk sudut yang lainnya. Sehingga kedua sudut terebut dapat disebut sebagai sudut yang saling berpelurus (suplemen).

Berikut adalah gambar untuk sudut berpelurus:

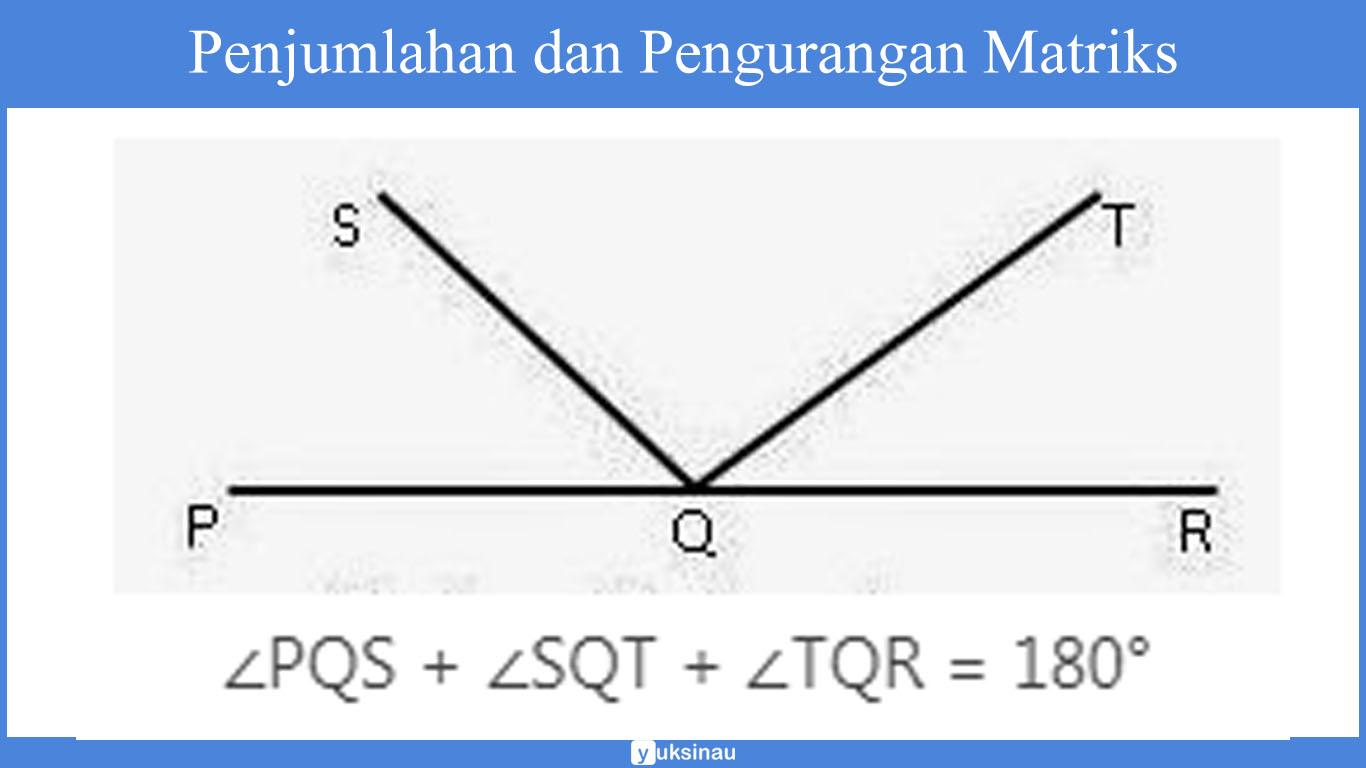
Jumlah dua sudut yang saling berpelurus (bersuplemen) yaitu 180°. Sudut yang satu adalah pelurus dari sudut yang lain.

Hubungan Antar Sudut apabila Dua Garis Sejajar

Dipotong oleh Garis Lain

Perhatikan baik-baik pada gambar di bawah ini:

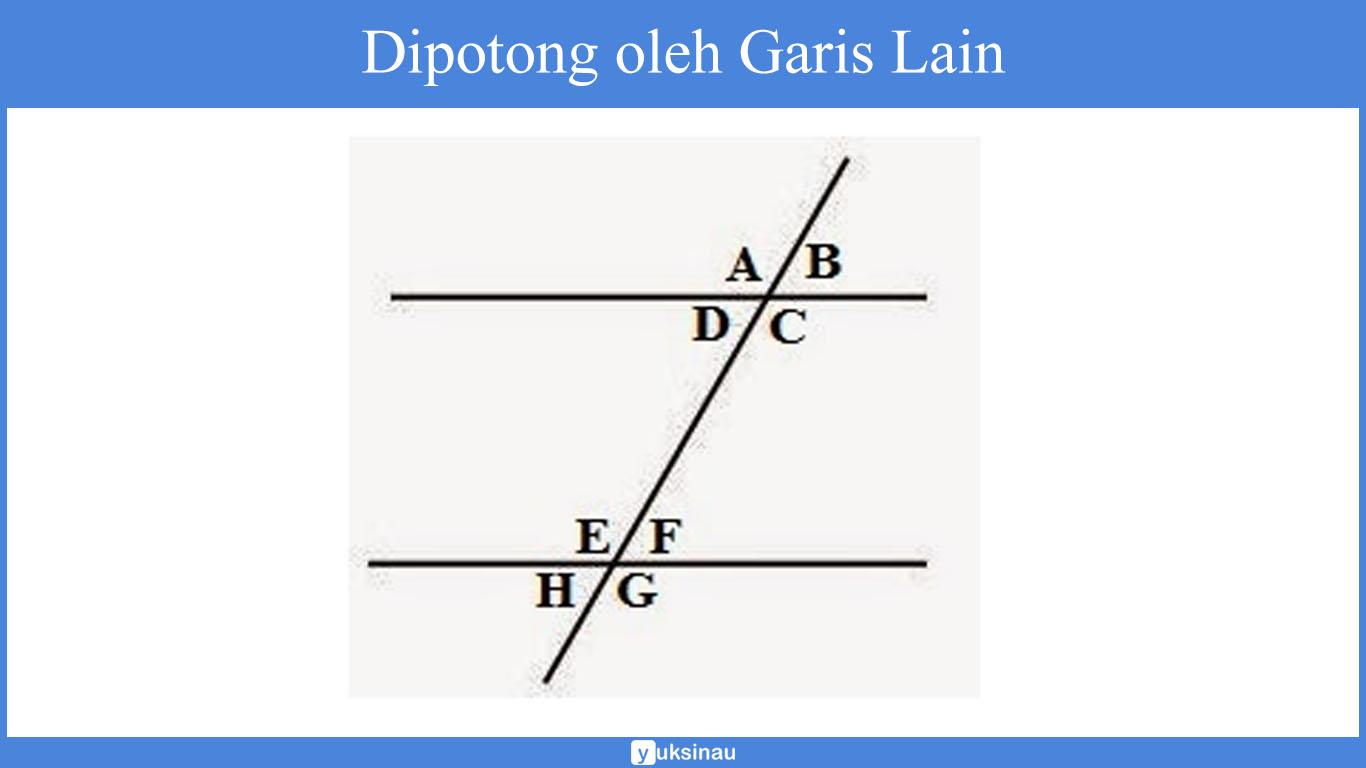
Sudut Sehadap (sama besar)

Merupakan suatu sudut yang mempunyai posisi yang sama serta besarnyapun sama. Pada gambar di atas, sudut yang sehadap yaitu:

∠A = ∠E
∠B = ∠F
∠C = ∠G
∠D = ∠H

Sudut Dalam Berseberangan (sama besar)

Merupakan sautu sudut yang terdapat dalam bagian dalam serta posisinya saling berseberangan. Dalam gambar di atas sudut dalam berseberangannya yaitu:

∠C = ∠E
∠D = ∠F

Sudut Luar Berseberangan (sama besar)

Merupakan suatu sudut yang terletak di bagian luar serta posisinya saling berseberangan, sebagai contoh:

∠A = ∠G
∠B = ∠H

Sudut-Sudut Sehadap dan Bersebrangan

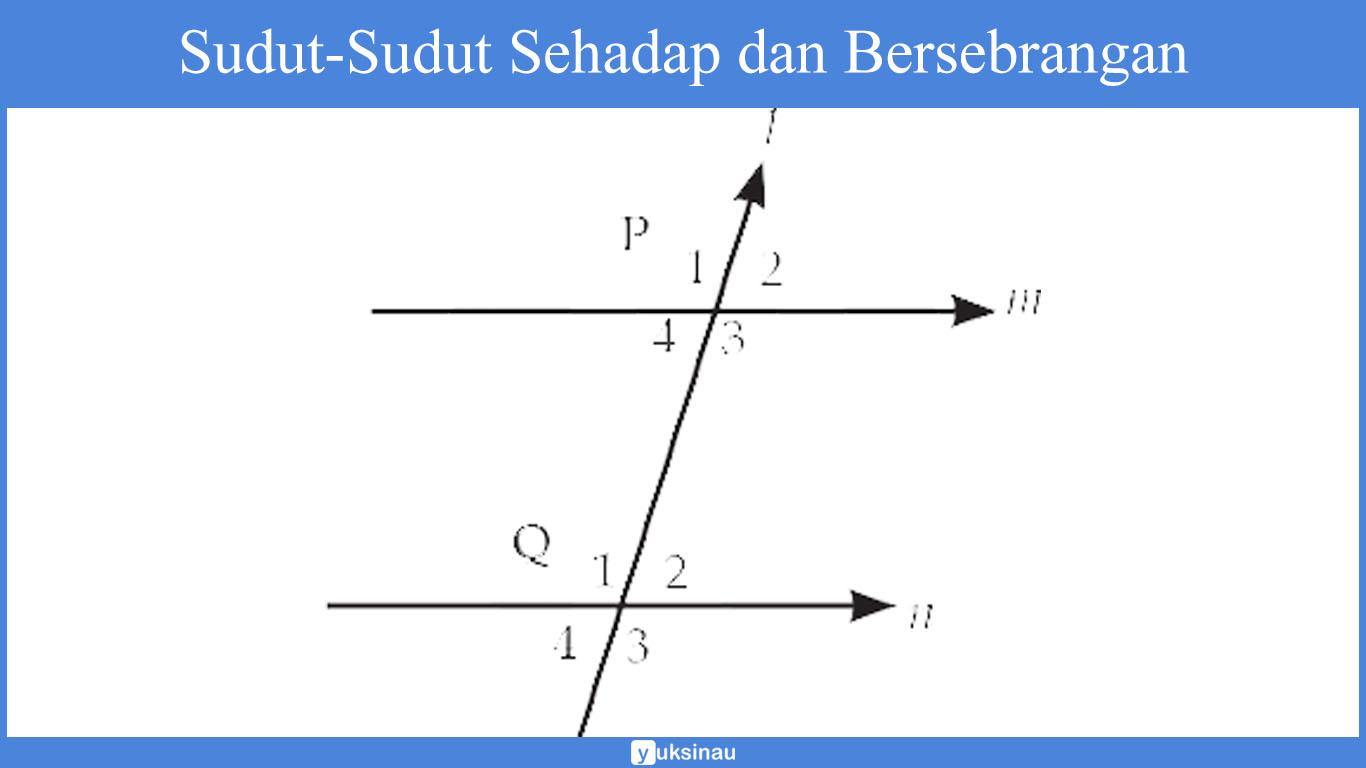
• Apabila dua buah garis sejajar dipotong oleh garis lain maka akan terbentuk empat pasang sudut sehadap yang besarnya sama.
• Apabila terdapat dua buah garis dipotong oleh garis lain maka besar dari sudut-sudut luar berseberangan yang terbentuk ialah  sama besar.
• Apabila terdapat dua buah garis sejajar dipotong oleh garis lain, besar sudut-sudut dalam berseberangan yang terbentuk ialah sama besar.
• Apabila terdapat dua buah garis sejajar dipotong oleh garis lain maka jumlah sudut-sudut dalam sepihak ialah 180°.

Sudut Dalam Sepihak

Merupakan sudut yang terletak di bagian dalam serta posisinya terletak pada sisi yang sama. Jika dijumlahkan, sudut yang saling sepihak akan membentuk sudut 180°. Sebagai contoh:

∠D + ∠E = 180°
∠C + ∠F = 180°

Sudut Luar Sepihak

Merupakan suatu sudut yang terletak di bagian luar serta posisinya terletak pada sisi yang sama. Jika dijumlahkan, sudut yang saling sepihak akan membentuk sudut 180°. Sebagai contoh:

∠B + ∠G = 180°
∠A + ∠H = 180°

Sudut bertolak belakang (sama besar)

Merupakan suatu sudut yang posisinya saling bertolak belakang, dalam gambar di atas, sudut yang bertolak belakang yaitu:

∠A = ∠C
∠B = ∠D
∠E = ∠G
∠F = ∠H

Pasangan sudut yang saling bertolak belakang terjadi apabila terdapat dua garis berpotongan sehingga dua sudut yang letaknya saling membelakangi titik potongnya disebut sebagai dua sudut yang bertolak belakang.
Dua sudut yang saling bertolak belakang merupakan sama besar.

Satuan Sudut

Pada dalam ukuran derajat, nilai 1 derajat mewakili suatu sudut yang diputar sejauh 1/360 putaran. Yang berarti 1°=1/360 putaran.

Untuk menyebutkan suatu ukuran sudut yang lebih kecil dari derajat (°) kita dapat memakai smbol menit (‘) dan juga detik (”).

Perhatikan baik-baik hubungan derajat, menit, dan detik di bawah ini:

1 derajat (1°) = 60 menit (60′)

1 menit (1′) = 1/60°

1 menit (1′) = 60 detik (60”)

1 derajat (1°) = 3600 detik (3600”)

1 detik (1”) = 1/3600°

Ukuran sudut dalam satuan radian

1° = p/180 radian

atau

1 radian = 180°/p

Jika nilai p = 3,14159 sehingga:

1° = p/180 radian = 3,14159/180 = 0,017453

atau

1 radian = 180°/p = 180°/3,14159 = 57,296°

Contoh Soal dan Pembahasan

Berikut akan kami berikan beberapa soal terkait garis dan sudut, diantaranya yaitu:

Soal 1.

Tiga buah garis masing-masing k, l dan m dalam susunan seperti gambar berikut.

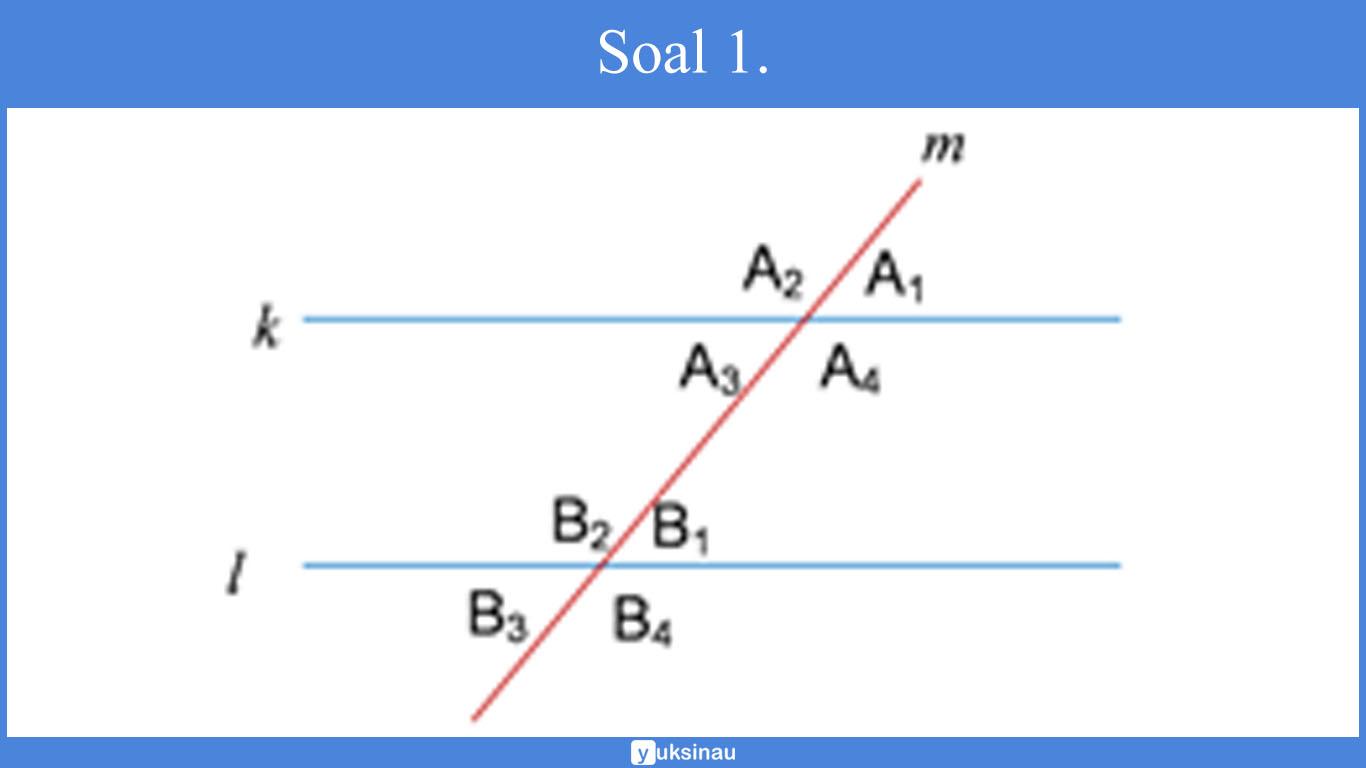
Garis k merupakan sejajar dengan garis l serta garis m memotong garis k dan l.

Maka, tentukanlah:

a) sudut-sudut yang sehadap
b) sudut-sudut yang bertolak belakang
c) sudut-sudut yang berseberangan dalam
d) sudut-sudut yang berseberangan luar
e) sudut-sudut dalam sepihak
f) sudut-sudut luar sepihak
g) sudut-sudut berpelurus

Jawab:

a) sudut-sudut sehadap yaitu:

∠A1 dengan ∠B1
∠A4 dengan ∠B4
∠A2 dengan ∠B2
∠B3 dengan ∠B3

b) sudut-sudut bertolak belakang yaitu:

∠A1 dengan ∠A3
∠A2 dengan ∠A4
∠B1 dengan ∠B3
∠B2 dengan ∠B4

c) sudut-sudut berseberangan dalam (dalam berseberangan) yaitu:

∠A3 dengan ∠B1
∠A4 dengan ∠B2

d) sudut-sudut berseberangan luar yaitu:

∠A2 dengan ∠B4
∠A1 dengan ∠B3

e) sudut-sudut dalam sepihak yaitu:

∠A3 dengan ∠B2
∠A4 dengan ∠B1

f) sudut-sudut luar sepihak yaitu:

∠A2 dengan ∠B3
∠A1 dengan ∠B4

g) sudut-sudut berpelurus yaitu:

∠A1 dengan ∠A2
∠A1 dengan ∠A4
∠A2 dengan ∠A3
∠A3 dengan ∠A4
∠B1 dengan ∠B2
∠B1 dengan ∠B4
∠B2 dengan ∠B3
∠B3 dengan ∠B4

Soal 2.

Diberikan tiga buah garis yakni k, l dan m dan juga sudut-sudut yang berada di lingkungannya. k dan l merupakan sejajar sementara garis m memotong garis k dan l.

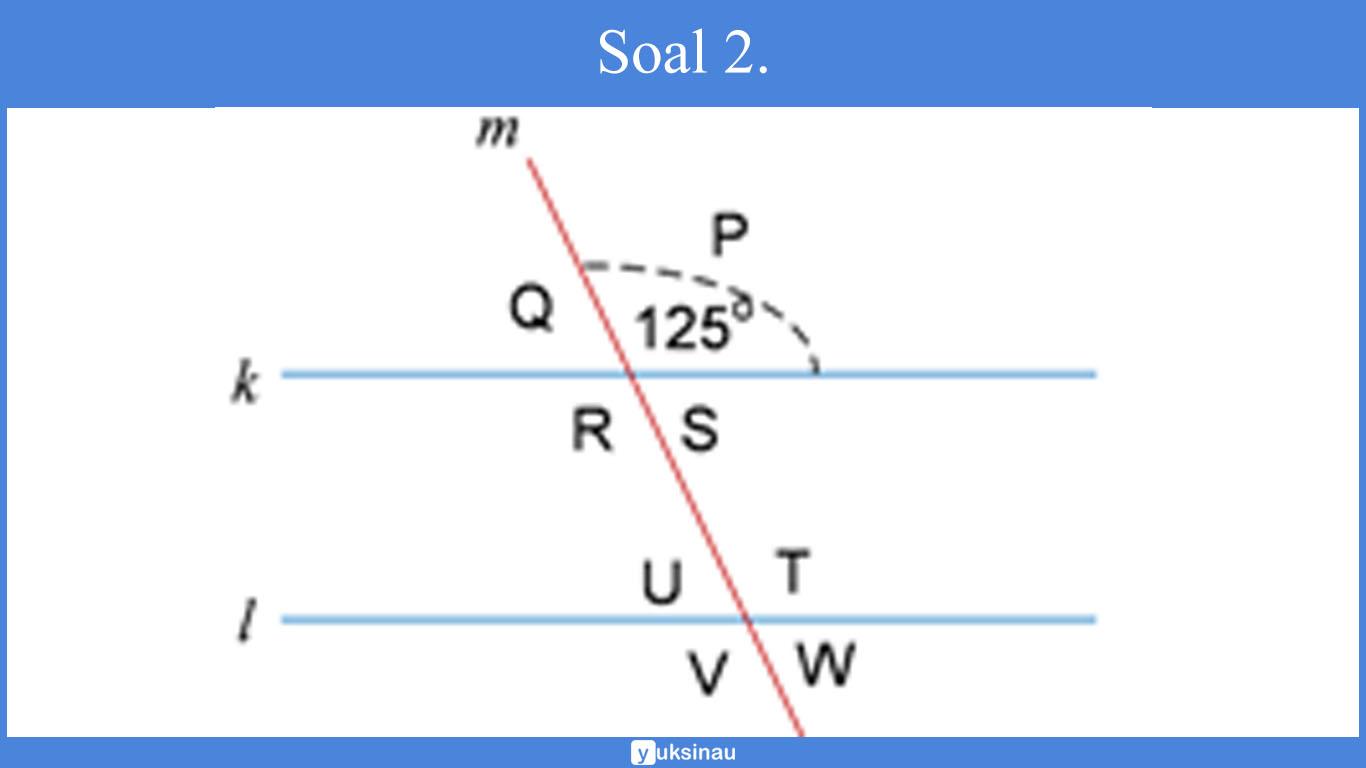
Apabila ∠ P = 125° , maka tentukanlah ketujuh sudut lain disekitarnya!

Jawab:

∠R = ∠P = 125° (Sebab R bertolak belakang dengan P)
∠T = ∠P = 125° (Sebab T sehadap dengan P)
∠V = ∠R = 125° (Sebab V sehadap dengan R)∠Q = 180° − ∠P = 180° − 125° = 55° (Sebab Q pelurus P)
∠S = ∠Q = 55° (Sebab S bertolak belakang dengan Q)
∠U = ∠Q = 55° (Sebab U sehadap dengan Q)
∠W = ∠ U = 55° (Sebab W bertolak belakang dengan U)

Soal 3.

Cermati gambar di bawah iini, apabila EF sejajar DG dan segitiga ABC adalah segitia sama kaki dengan besar sudut C ialah 40°.

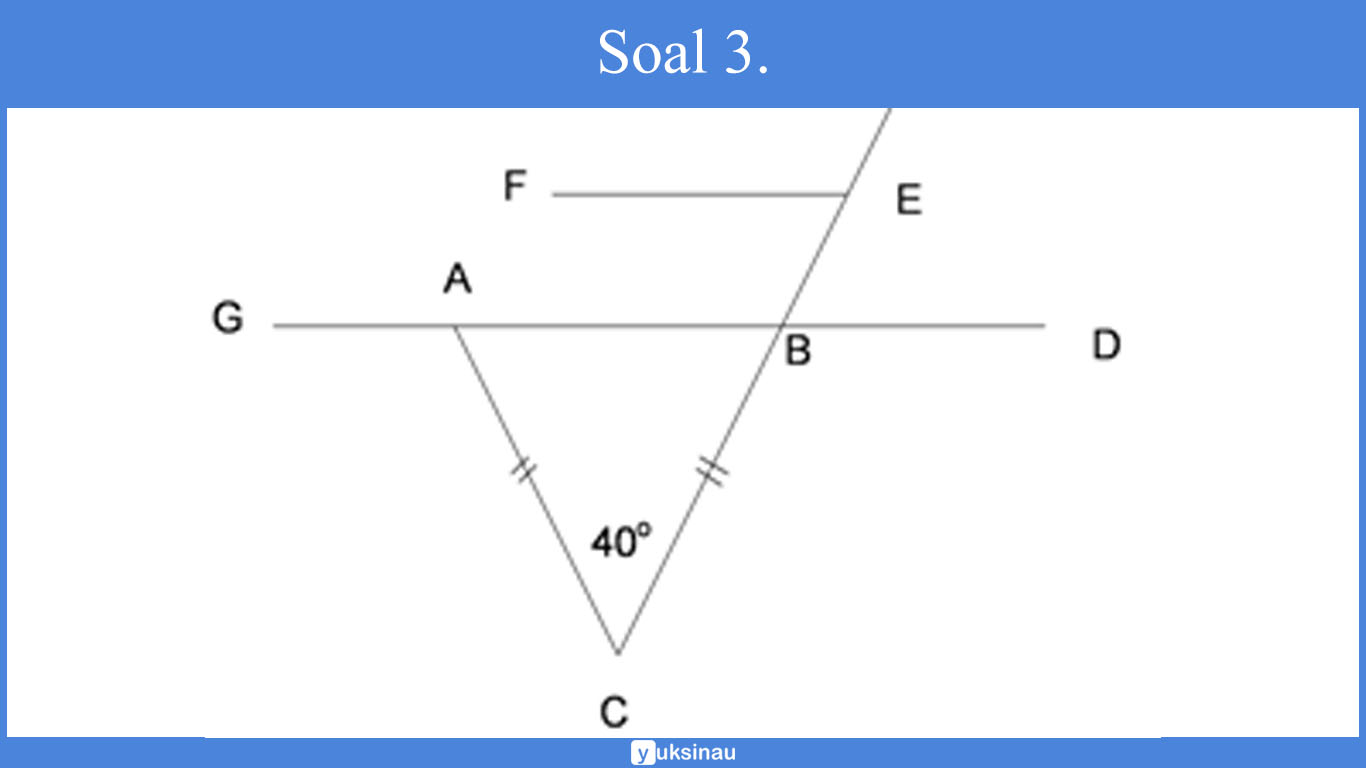
Maka tentukan:

a) Besar sudut DBE
b) Besar sudut BEF
c) Besar sudut CAG

Jawab:

a) Besar sudut DBE

Langkah pertaama adalah mencari terlebih dahulu besar sudut ABC.Δ ABC merupakan segitiga sama kaki sehingga besar ∠ABC = ∠BAC.Tiga sudut dalam suatu segitiga apabila kita jumlahkan adalah 180° sehingga,∠ABC = (180 − 40) : 2 = 70° dengan begitu ∠BAC juga 70°∠DBE = ∠ ABC = 70° karena keduanya bertolak belakang.

b) Besar sudut BEF

∠BEF = ∠ABC = 70° sebab keduanya sehadap atau  ∠BEF = ∠ DBE = 70° sebab keduanya berseberangan.

c) Besar sudut CAG

∠CAG = 180 − ∠BAC = 180 − 70 = 110°, sebab CAG serta BAC berpelurus.

Soal 4. (UN 2012/2013 paket 54)

Perhatikan gambar di bawah ini!

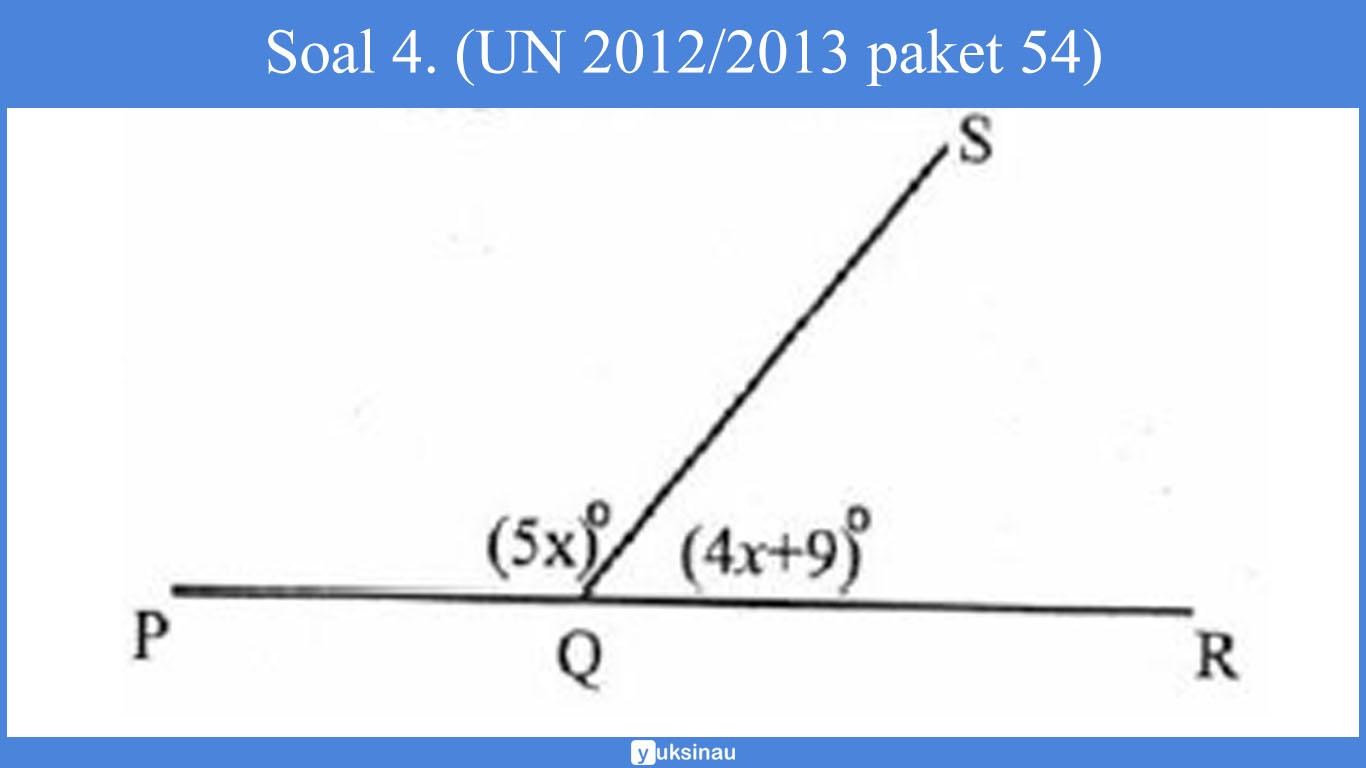
Besar pelurus sudut SQR adalah ….

1. 101°
2. 100°
3. 95°
4. 92°

Jawab:

Perhatian** soal ini adalah salah satu soal jebakan, banyak yang mengira jika soal tersebut menanyakan ∠SQR padahal yang diminta yaitu ∠PQS.

Untuk menjawab soal ini hal pertama yang harus kalin cari yaitu nilai x.

Dalam hal ini ∠PQS serta ∠SQR adalah sudut saling pelurus, sehingga:

∠PQS + ∠SQR = 180°(5x)° + (4x+9)° = 180°9x° + 9 = 180°9x° = 171°x° = 19°

 

Pelurus ∠SQR = ∠PQSPelurus ∠SQR = (5x)°Pelurus ∠SQR = (5.19)°Pelurus ∠SQR = 95° (Jawaban C)

Soal 5. (UN 2009/2010 paket 10)

Perhatikan gambar berikut ini:

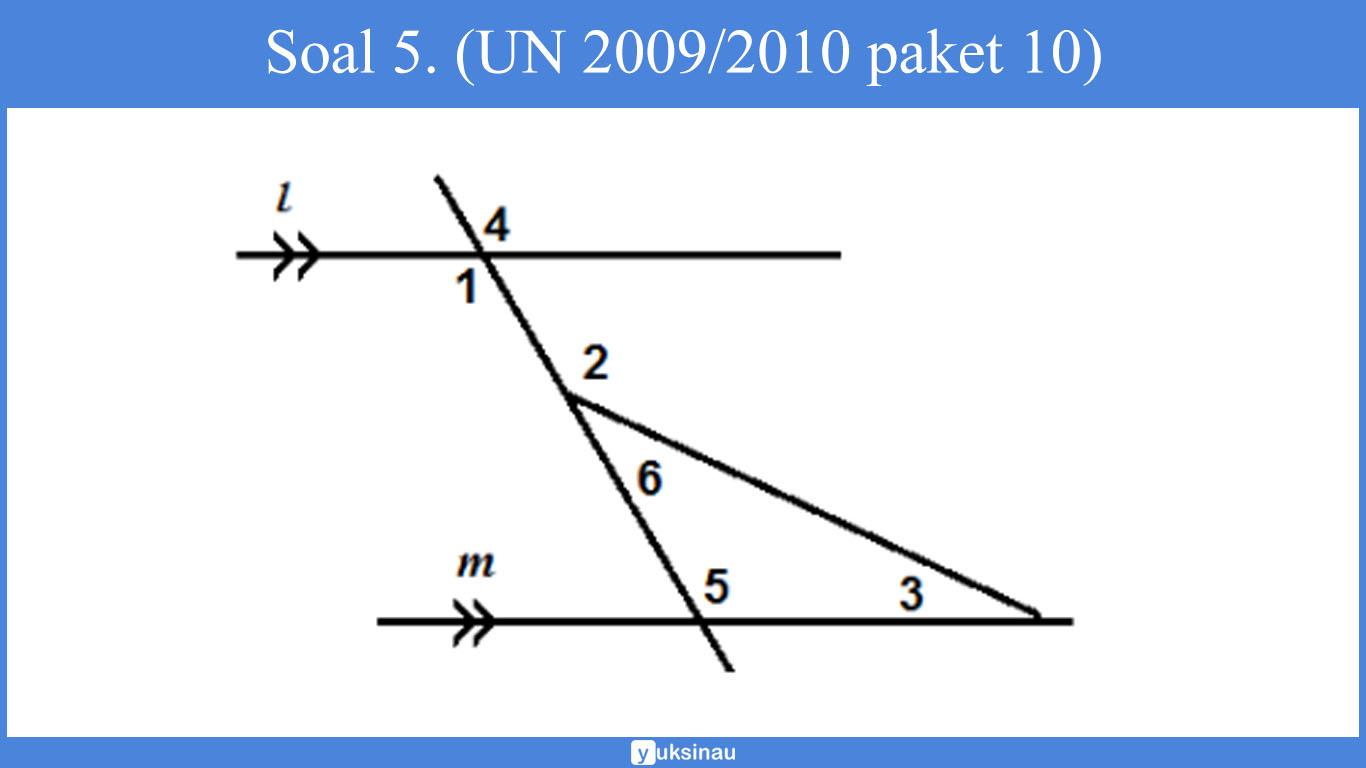
Besar sudut nomor 1 adalah 95°, dan besar sudut nomor 2 adalah 110°. Besar sudut nomor 3 adalah ….

1. 5°
2. 15°
3. 25°
4. 35°

Jawab:

∠1 = ∠5 = 95° (sudut dalam berseberangan)∠2 + ∠6 = 180° (saling berpelurus)110° + ∠6 = 180°∠6 = 70°∠5 + ∠6 + ∠3 = 180°95° + 70° + ∠3 = 180°165° + ∠3 = 180°∠3 = 15° (Jawaban B)

Soal 6. (UN 2010/2011 paket 15)

Perhatikan gambar di bawah ini:

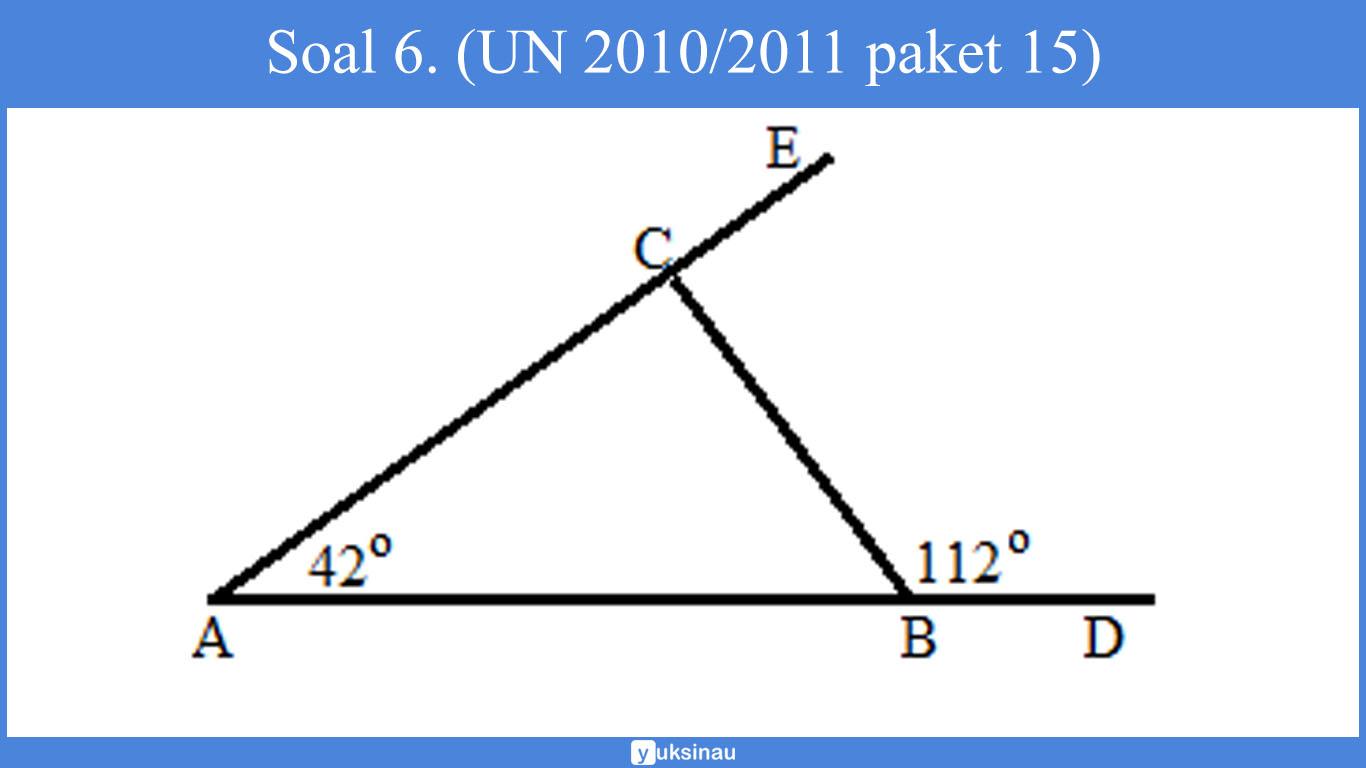
Besar ∠BCA adalah ….

1. 70°
2. 100°
3. 110°
4. 154°

Jawab:

∠ABC + ∠CBD = 180° (saling berpelurus)∠ABC + 112° = 180°∠ABC = 68°∠BCA + ∠ABC + ∠BAC = 180°∠BCA + 68° + 42° = 180°∠BCA + 110 = 180°∠BCA = 70° (Jawaban A)

Soal 7. (UN 2010/2011 paket 15)

Perhatikan gambar di bawah ini:

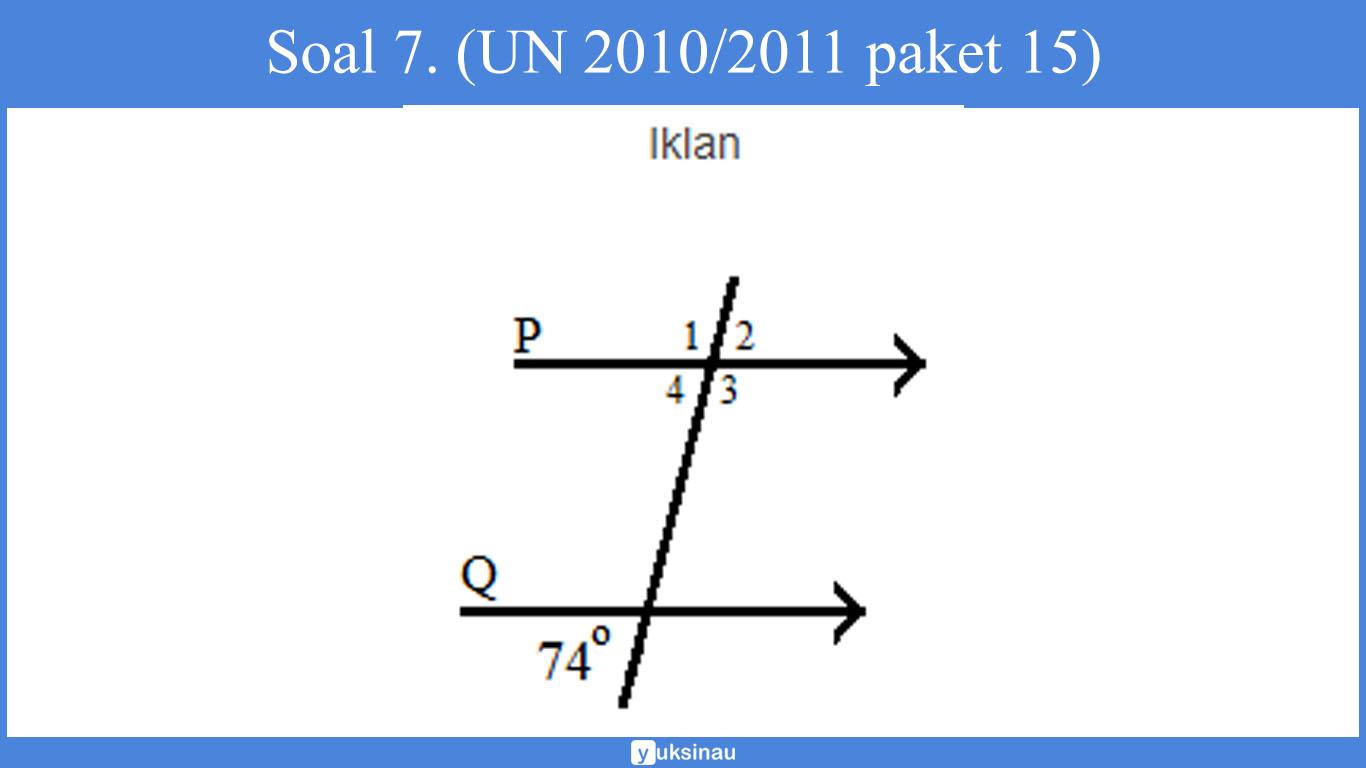
Besar ∠P3 adalah ….

1. 37°
2. 74°
3. 106°
4. 148°

Jawab:

∠P2 = 74° (sudut luar berseberangan)∠P2 + ∠P3 = 180° (saling berpelurus)74° + ∠P3 = 180°∠P3 = 106° (Jawaban C)

Soal 8. (UN 2012/2013 paket 1)

Perhatikan gambar di bawah ini:

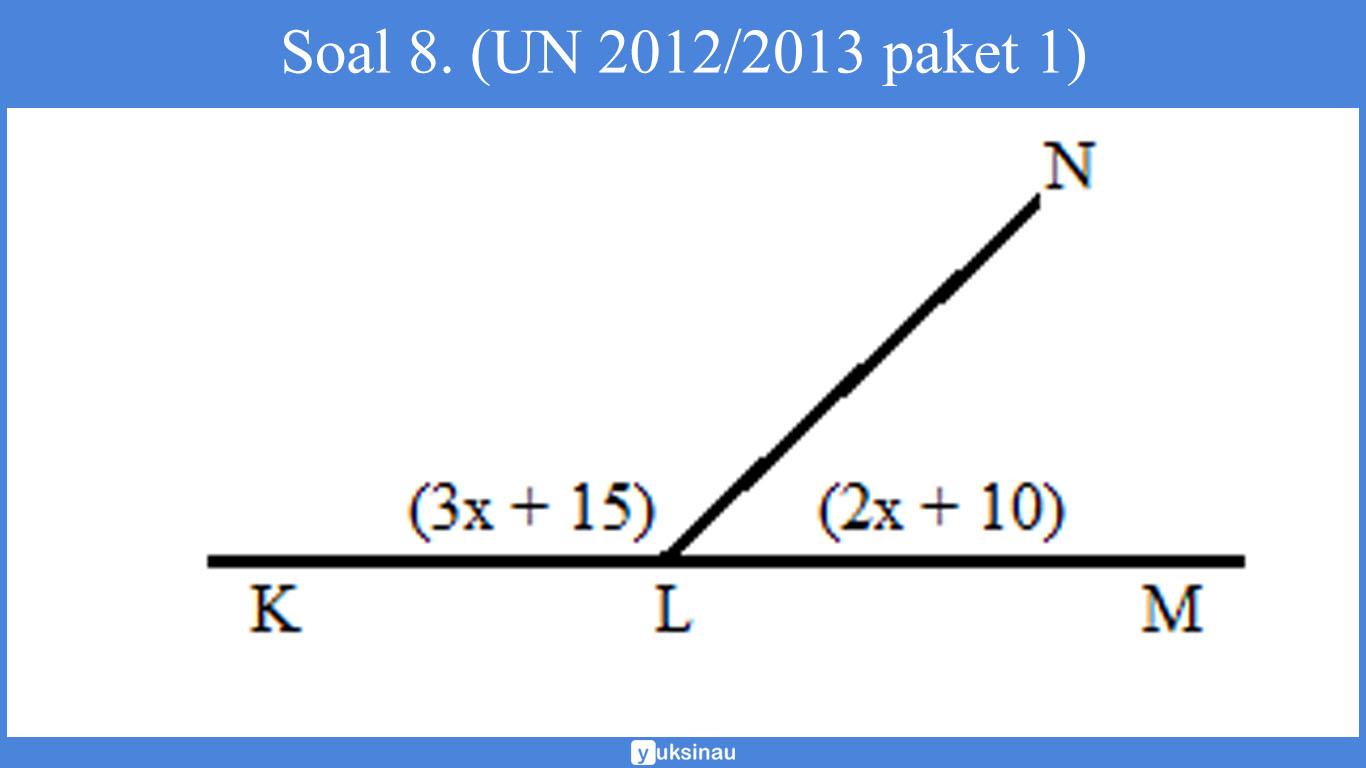
Besar pelurus sudut KLN adalah ….

1. 31°
2. 72°
3. 85°
4. 155°

Jawab:

Untuk menjawab soal ini langkah pertama yang harus kalian cari yaitu nilai x.

Dalam soal tersebut ∠KLN dan ∠MLN adalah sudut saling pelurus, sehingga:

∠KLN + ∠MLN = 180°(3x + 15)° + (2x+10)° = 180°5x° + 25° = 180°5x° = 155°x° = 31°

 

Pelurus ∠KLN = ∠MLNPelurus ∠KLN = (2x+10)°Pelurus ∠KLN = (2.31 + 10)°Pelurus ∠KLN = 72° (Jawaban B)

Soal 9. (UN 2012/2013 paket 2)

Perhatikan gambar di bawah ini:

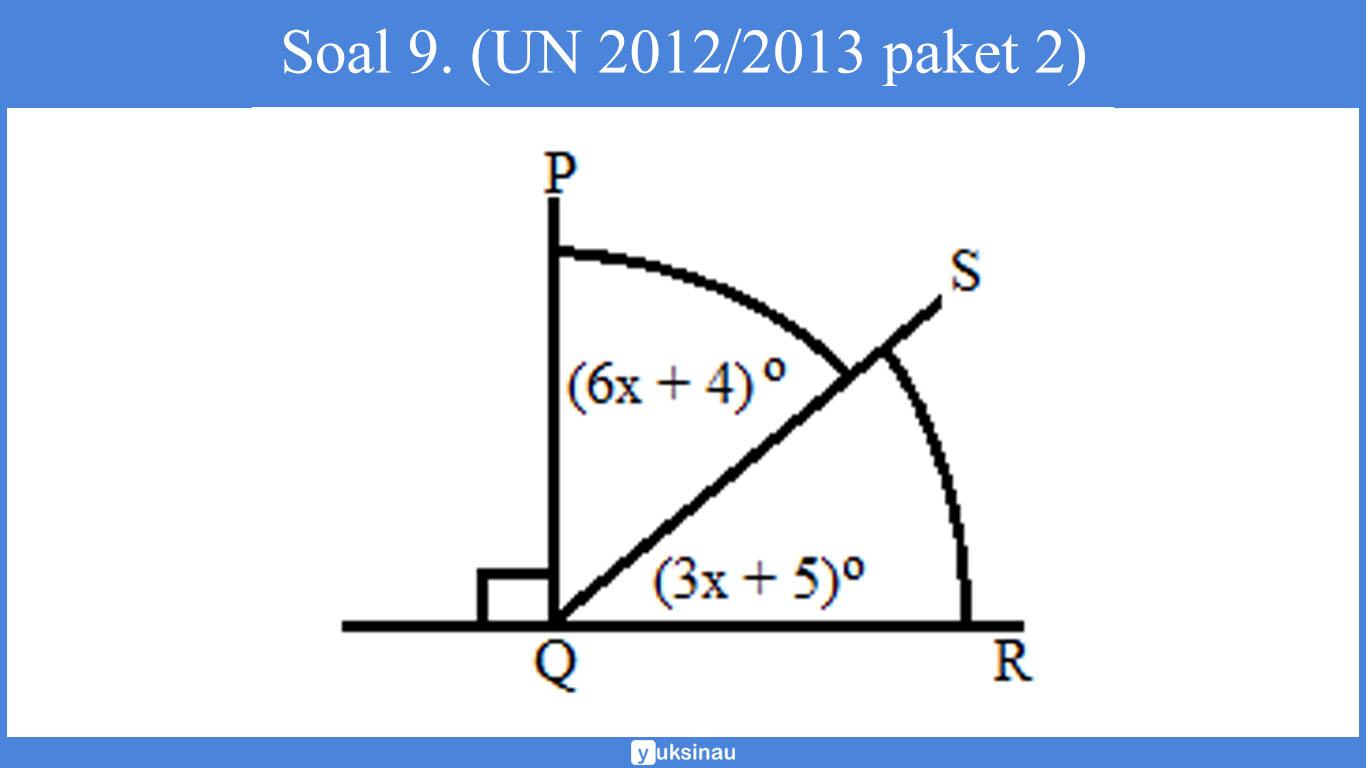
Besar penyiku ∠SQR adalah ….

1. 9°
2. 32°
3. 48°
4. 58°

Jawab:

Perhatian** soal ini adalah soal jebakan juga, sehingga banyak yang mengira jika soal tersebut menanyakan ∠SQR padahal yang diminta ialah ∠PQS.

Untuk menjawab soal ini langkah pertama yang harus kalian cari yaitu nilai x.

Dalam soal tersebut ∠SQR dan ∠PQS adalah sudut saling berpenyiku, sehingga:

∠SQR + ∠PQS = 90°(3x + 5)° + (6x+4)° = 90°9x° + 9° = 90°9x° = 81°x° = 9°

Penyiku ∠SQR = ∠PQSPenyiku ∠SQR = (6x+4)°Penyiku ∠SQR = (6.9 + 4)°Penyiku ∠SQR = 58° (Jawaban D)

Soal 10. (UN 2012/2013 paket 5)

Perhatikan gambar di bawah ini:

Besar pelurus ∠AOC adalah ….

1. 32°
2. 72°
3. 96°
4. 108°

Jawab:

Untuk menjawab soal nomor 10, langkah pertama yang harus kalian cari yaitu nilai x.

Dalam soal tersebut ∠AOC dan ∠BOC adalah sudut saling pelurus, sehingga:

∠AOC + ∠BOC = 180°(8x – 20)° + (4x+8)° = 180°12x° – 12° = 180°12x° = 192°x° = 16°

 

Pelurus ∠AOC = ∠BOCPelurus ∠AOC = (4x+8)°Pelurus ∠AOC = (4.16 + 8)°Pelurus ∠AOC = 72° (Jawaban B)

Baca juga: Aritmatika Sosial

Demikianlah ulasan singkat kali ini mengenai Garis dan Sudut yang dapat kami sampaikan. Semoga ulasan di atas mengenai Garis dan Sudut dapat kalian jadikan sebagai bahan belajar kalian.

The post Garis dan Sudut appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Semoga saja pembahasan Garis dan Sudut - Yuk Sinau diatas bisa menambah wawasan kita semua. Tak lupa kami ucapkan banyak-banyak terima kasih sudah berkunjung ke situs chipcoid. blogspot. com dan membaca uraian diatas hingga selesai. Sampai ketemu di postingan selanjutnya dan jangan lupa bahagia.