Rumus Bangun Ruang - Pak Dosen
Memang cukup menarik bila kita membahas mengenai Rumus Bangun Ruang terlebih untuk Anda yang saat ini memang sedang mencarinya. Seperti yang tertulis pada judul kita akan membahas tentang "Rumus Bangun Ruang" secara lengkap, mulai dari awal hingga akhir dan kami menyusunnya sedemikian rupa supaya para pembaca dapat dengan mudah memahaminya. Baiklah yuk langsung disimak saja.
Uraian Lengkap Rumus Bangun Ruang
Selamat datang di Pakdosen.co.id, web digital berbagi ilmu pengetahuan. Kali ini PakDosen akan membahas tentang Bangun Ruang? Apakah kalian pernah mendengar istrilah dari Bangun Ruang? Jangan khawatir jika kalian belum pernah mendengarnya, disini PakDosen akan membahas secara rinci tentang macam, rumus dan gambar. Simak Penjelasan berikut secara seksama, jangan sampai ketinggalan.
Bangun ruang adalah penyebutan untuk bangun-bangun 3 dimensi atau bangun yang memiliki ruang yang dibatasi oleh sisi-sisinya. seperti dikutip suratkabar.id
Perlu anda ketahui, bahwa volume sebuah bangun ruang sebagai daya tampung perhitungan ukuran banyak ruang yang dapat ditempati dalam sebuah objek. Dimana objek tersebut merupakan berupa benda yang tersusun maupun yang tidak tersusun.
Contoh dari benda yang tersusun seperti kerucut, bola, tabung atau silinder, limas, kubus dan balok. Selain dapat dihitung besar volumenya, sebuah bangun ruang juga bisa dihitung luas permukaannya. Sehingga bisa diketahui bahwa rumus bangun ruang melingkupi volume dan luas permukaan.
Macam-Macam Bangun Ruang
dikutip dari laman chip.co.id Berikut ini terdapat beberapa macam-macam bangun ruang dan rumus, yakni sebagai berikut :
#1. Kubus
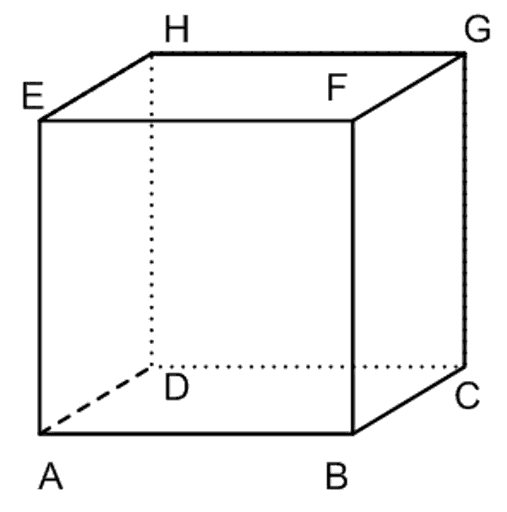
Bangun ruang kubus terdiri dari 6 sisi yang sama yaitu berbentuk persegi, yang tentunya ke 6 sisinya adalah bangun datar persegi dengan luas yang sama besar.
Kubus juga terbentuk atas 12 rusuk dengan panjang yang sama besar.
Dan untuk sudut kubus, semua sudut kubus bernilai 90 derajat atau semuanya berbentuk siku-siku.
Rumus Kubus:
- Luas permukaan kubus:
6 x luas sisi = 6 x rusuk x rusuk
- Panjang diagonal ruang:
akar dari (3 x rusuk kuadrat)
- Volume Kubus:
rusuk x rusuk x rusuk = rusuk^3
#2. Balok
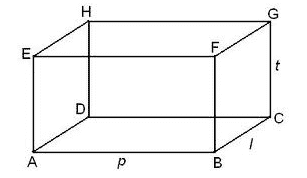
Bangun ruang balok memiliki 6 buah sisi, dimana dua buah sisi yang berhadapan sama besar. Jadi ada 3 sisi yang saling berhadapan satu sama lain dimana untuk balok minimal harus memiliki satu sisi saling berhadapan yang berbeda dengan sisi saling berhadapan yang lain.
Balok memiliki 12 rusuk seperti kubus, dimana memiliki rusuk dengan perwakilan panjang, lebar dan tinggi. Untuk ukuran panjang, lebar, dan tinggi semuanya tidak sama panjang atau minimal salah satu tidak sama panjang.
Untuk sudut, sama dengan kubus, yaitu memiliki semua sudut dengan besar 90 derajat atau siku-siku.
Rumus Balok:
- Luas Permukaan Balok:
2 x { (pxl) + (pxt) + (lxt) }
- Panjang diagonal ruang:
akar dari (p kuadrat + l kuadrat + t kuadrat)
- Volume Balok:
p x l x t
Keterangan:
p = panjang
l = lebar
t = tinggi
#3. Prisma
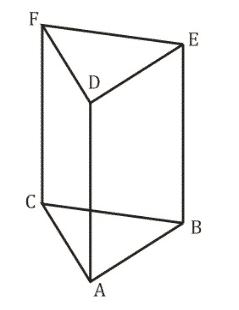
Bangun prisma dibedakan menjadi beberapa macam, dimana penamaan Bangun ruang Prisma tergantung dari bentuk alasnya.
Misal ketika sebuah prisma memiliki alas berbentuk segitiga, maka disebut Prisma Segitiga. Prisma lainnya adalah Prisma Segi Empat (bukan balok), Prisma Segi Lima, dll.
Rumus Prisma:
- Luas Permukaan Prisma
= luas alas + luas selimut + luas atap
= ( 2 x luas alas) + (kell alas x tinggi)
- Volume Prisma:
luas alas x tinggi
Keterangan:
La = luas alas
K = keliling alas
t = tinggi prisma
- Rumus Prisma Segitiga Siku-siku
Luas Permukaan Prisma Segitiga Siku-Siku:
= (2 x luas segitiga siku2) + (kell segita siku2 x t)
= (alas segitiga x tinggi segitiga) + (kell segita siku2 x t)
- Volume Prisma:
1/2 x alas x tinggi x tinggi prisma
#4. Tabung
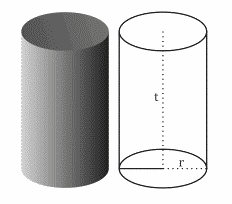
Tabung bisa kita katakan juga sebuah prisma, tetapi tabung memiliki penamaan sendir karena alasnya yang berbentuk lingkaran atau tidak bersegi.
Rumus Tabung:
- Luas Permukaan Tabung:
= luas alas + luas selimut + luas tutup
= luas lingkaran + luas segi empat + luas lingkaran
= (2 x luas lingkaran) + luas segi empat
= { (2 x π x r^2) + (π x d x t) }
- Volume Tabung:
= luas alas x tinggi
= luas lingkaran x t
= π x r^2 x t
#5. Limas
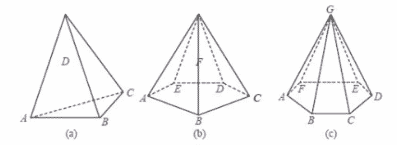
Bangun ruang limas, sebenarnya sama halnya dengan Bangun Ruang Prisma, dimana dibedakan menjadi beberapa macam karena bentuk alas yang berbeda-beda. Diantaranya adalah Limas Segitida, Limas Segi Empat, Limas Segi Lima, Dll.
Rumus Limas:
- Luas Permukaan Limas:
luas alas + jumlah luas sisi tegak
- Volume Limas:
1/3 x Luas alas x tinggi
Rumus Limas Segi Empat:
- Luas Limas Empat:
luas alas + 4 x luas sisi tegak
- Volume Limas Empat:
1/3 x Luas alas x tinggi
#6. Kerucut
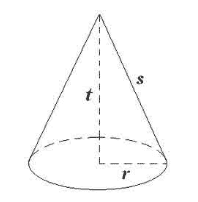
Kerucut bisa dikatakan sebuah Limas, dimana dikatakan kerucut karena alasnya yang berbentuk lingkaran, ini sama halnya hubungan Prisma dengan Tabung.
Rumus Kerucut:
- Luas Permukaan Kerucut:
= Luas alas + Luas Selimut
= π r^2 + π r s = π r (r + s)
- Volume Kerucut:
= 1/3 x Luas alas x tinggi
= 1/3 x π x r x r x t = 1/3 x π x r^2 x t
Keterangan:
r = jari2 alas/lingkaran
s = panjang garis pelukis kerucut
t = tinggi kerucu
Tambahan:
volume kerucut = volume setengah bola
1/3 π r² t = 1/2 4/3 π r³
1/3 π r² 2r = 2/3 π r³
2/3 π r³ = 2/3 π r³
#7. Bola
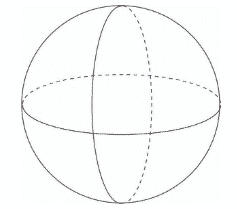
Bola merupakan bangun ruang yang sangat menarik, dimana adalah bangun ruang yang tidak memiliki segi, sama halnya dengan lingkaran di pembahasan bangun datar/2 dimensi.
Rumus Bola:
- Luas Permukaan Bola:
= Luas 4 lingkaran
= 4 x luas lingkaran
= 4 x π r ^2
- Volume Bola:
4/3 π r^3
Demikian Penjelasan Materi Tentang 7 Macam-Macam Bangun Ruang Beserta Rumus dan Gambar
Semoga Materinya Bermanfaat Bagi Siswa-Siswi
The post Rumus Bangun Ruang first appeared on PAKDOSEN.CO.ID.
ARTIKEL PILIHAN PEMBACA :
Comments
Post a Comment